Farbsysteme - Einleitung

Kanäle

Da unser Auge mit drei verschiedenen Farbrezeptoren arbeitet (tri-chromatisch) braucht es für die numerische Darstellung einer Farbe drei Zahlen respektive Kanäle zu deren Übetragung. Dabei gibt es verschiedene Varianten. Die wichtigsten sind.

RGB und CMY

Additives und Subtraktives Farbmodell (Mischfarben).

HSL/HSV

Farbangabe gemäss Farbkreis und zwei Komponenten für Intensität und Graustufe.

Y*

Zerlegung in Luminanz (Schwarz-Weiss-Kanal) und zwei Farbanteile/abweichungen. Vor allem bei analogen Fernsehsignalen verbreitet. Abwärtskompatibel zu Schwarz-Weiss-Fernseher.

Wertbereiche

Viele Farbsysteme haben Untervarianten die sich in erster Linie durch die (obere) Grenzen der einzelnen Komponenten unterschieden. Typische Wertbereiche sind:

0 … 1

Für Berechnungen meist die einfachste Variante.

0 … 100%

Für den Menschen am besten lesbar.

0 … 255

meist vom Computer intern verwendet, da dies gerade einer 8Bit Information entspricht (nur ganzzahlige Werte erlaubt).

0 … 360°

Bei zyklischen Kanälen gerne verwendet, da es das bekannte Gradsystem der Winkel verwendet. → Farbrad (hs*-Systeme)

Darstellung & Speicherung

Weitere Varianten beziehen sich auf die Darstellung respektive Speicherung. Für uns am besten lesbar sind drei einzelne dezimale Zahlen. Der Computer bevorzugt aber einen einzelnen ganzzahligen Wert, der dann meist hexadezimal dargestellt wird. Dies geschieht durch addieren der einzelnen Kanäle mit einem entsprechenden Vorfaktor. Beispiel: die Komponenten des rgb Codes r:255 g: 127 b:0 werden nach der Formel red × 256² + blue × 256¹ + green × 256⁰ zusammengezählt. Im Beispiel ergibt das 255 × 256² + 127 × 256 + 0 × 1 = 16744192 oder als Hexadezimalzahl #FF7F00  . Hier erkennt man gut, das die ersten beiden Ziffern (FF) dem Wert 255 im roten Kanal entsprechen, die zweiten zwei dem blauen und die letzten beiden dem grünen Kanal.

Umrechnung Ganzzahlen ↔ Fliesskommazahlen

Farben werden meist als Ganzzahlen gespeichert (Integer mit meist 8Bit pro Kanal) bei Berechnungen sind aber Fliesskommazahlen oft besser. Beim Umrechnen der Fliesskommazahl in die zu speichernde Ganzzahl sollte nicht die naheliegende Formel v_8Bit = runden(v_0…1 × 255) verwendet werden. Den bei dieser Formel erhalten die beiden Werte #00 und #FF je nur halb soviel Platz wie alle anderen dazwischen, da jeweils die Hälfte ihres Rundungsbereich gar nie vorkommt. Die nächste Vermutung v_8Bit = abrunden(v_0…1 × (255+1)) führt zum Problem, dass der Wert 1 zum Wert #100 wird und somit zu gross ist. Deshalb wird hier mit folgender Formel gearbeitet. v_8Bit = abrunden(v_0…1 × (255+0.99999)).
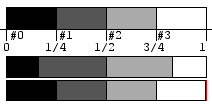
Das Bild rechts zeigt die Unterschiede der Verfahren anhand einer 2Bit Grauskala.

Transparenz, Alphakanal

Häufig wird einer Farbangabe ein weiterer vierter Kanal hinzugefügt, der die Transparenz beschreibt (Alphakanal). Die Farbe an sich ändert sich dabei vorerst nicht. Erst wenn zwei Farben (respektive Bilder) übereinander gelegt werden, entscheidet die Transparenz, wie viel der unteren Farbe durchscheint. Bei Null Transparenz kommt die obere Farbe vollständig zur Geltung, bei voller Transparenz die untere.

Beim Beispiel links wurde der ursprüngliche weisse Hintergrund rund um die beiden Kokosnuüsse mit einer unvollständigen Transparenz versehen. Dadurch scheinen die Farben des Hintergrundbildes hindurch, werden aber vom Weiss des Vordergrundbildes aufgehellt. Bei den beiden Nüssen selbst ist die Transparenz auf 0 gesetzt, wodurch der Hintergund vollständig überdeckt wird. Dies auch dort, wo das Fruchtfleisch selbst ebenso weiss ist wie der Hintergrund rundherum.

Nicht alle Grafikformate können mit Transparenz umgehen. Die bekanntesten Vertreter die einen Alphakanal haben (können) sind png und gif. Das für Fotos verwendet jpeg kennt keine Transparenz.

Eine Grafikprogramme wie Gimp arbeiten sogar mit je einem Transparenzkanal pro Farbkanal. Man kann also die Durchlässigkeit der Farbe Rot anders setzen als die von Blau.

Farbtabellen

Farbtabellen sind Sammlungen von Farben, teilweise inklusive einem zugehörigen Farbnamen. Einige Farbtabellen sind standardisiert, andere werden ad-hoc gebildet. Für die Verwendung von Farbtabellen gibt es mehrere Gründe:

• Vor allem in den frühen Tage der IT war Speicherbedarf und Rechenzeit teuer, weshalb man sich auf eher wenige Farben beschränkte. Dazu wurden zum eine standardisierte Farbtabellen (beispielsweise VGA) erstellt oder eine speziell auf ein Bild zugeschnitte Indextabelle verwendet.
• Webseiten und Programme ordnen oft einer Farbe eine Bedeutung oder Verwendung zu. Im folgenden wird eine Farbe nicht mehr über ihre Farbangabe sondern über ihren Zweck (Titelfarbe, Warnfarbe) angesprochen. Dies erleichtert Änderungen im Design, da diese zentral an einem Ort erledigt werden können. Dieses funktionale oder deklarative Denken ist auch zentraler Bestandteil von CSS-Definitionen für Webseiten.
• Programme die Diagramme erstellen haben meist eine vordefinierte Abfolge in der Farben standardmässig verwendet werden. Ein typisches Beispiel ist hier Excel.
• 
  Bei der Herstellung von Produkten ist das Einfärben des Produktes oft nicht einfach, insbesonder wenn Ansprüche bezüglich Wetterbeständigkeit, Krazfestigkeit und anderem hoch sind. Einige Hersteller nutzen deshalb eigene oder Branchenspezifische Farbtabellen, die dem Kunden die Möglichkeiten aufzeigen. Durch diese Standardisierung kann auch die Produktion und somit der Preis optimiert werden.
  Bekannte Vertreter sind hier RAL- oder HKS- oder Pantone Farben.
  Es ist anzumerken das bei solchen Farben eine perfekte Umwandlung in den rgb-Code des Computers nicht immer gelingen kann, da die Realität doch um einiges Vielfältiger ist, als was der Computer erträgt. Als Beispiel seien hier Metalic- oder Leucht-Effekte erwähnt, die man bei reelen Farben haben kann, nicht aber auf dem Computer.

Ein grosses Verzeichnis an Farbtafeln und Namen findet sich auch bei Jaffer.