
An einem 500m langen Strand steht am einen Ende ein Glacéstand. Im Schnitt kaufen die Gäste alle drei Stunden ein Glacé, wenn sie in unmittelbarer Nähe des Standes ihren Platz haben. Pro 100m Distanz warten sie zusätzliche 20 Minuten. Wie viel Glacé wird innert 4 Stunden verkauft, wenn pro Meter Strand 2 Personen liegen? Die Breite des Strandes darf vernachlässigt werden.
Bei dieser Aufgabe enstehen lustige Einheiten wie Glacé×Meter/Personen×Stunde und das erst noch durch Integration, die normalerweise vor allem für m² gebraucht wird. Aber fangen wir vorne an.
Direkt beim Stand liegt die Zeit zwischen zwei Glacékäufen bei 120min, am anderen Ende des Strandes (+5×20m) bei 220min, oder als Funktion geschrieben:
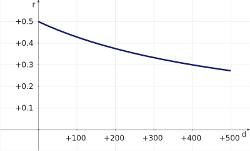
Die Einheit dieser Wartezeit ist [min]. Für das gesuchte Ergebnis ist aber die Einheit [1/h] notwendig. Diese erreicht man durch Kehrtert bilden und mit 60 multiplizieren. r(d) sind die Anzahl verkaufte Glacé pro Stunde und Person, als Funktion der Distanz zum Glacéstand (Funktionsplot rechts):
Als nächstes wird diese Funktion von 0 bis 500m integriert. Das Ergbenis hat die leicht seltsame Einheit von [Glacée×Meter pro Personen×Stunde]. Aber das bestimmte Integral berechnet die Fläche unter der Kurve. Und genau wie bei der Flächenberechnung eines Blatt Paier hat das Ergbenis als Dimension das Produkt aus der horizontalen und vertikalen Achse. Beim Papier sind das beide mal [cm], hier sind es [Glacée pro Personen×Stunde] und Meter.
Für das Endergebnis muss jetzt nur noch mit der Strandbelegung (2 Personen pro Meter) und der Gesamtzeit (4h) multipliziert werden. Das ergibt aufgerundet 1'455 verkaufte Glacés.
Anmerkung: Die Idee der Aufgabe basiert auf einer Problemstellung aus der Spieltheorie